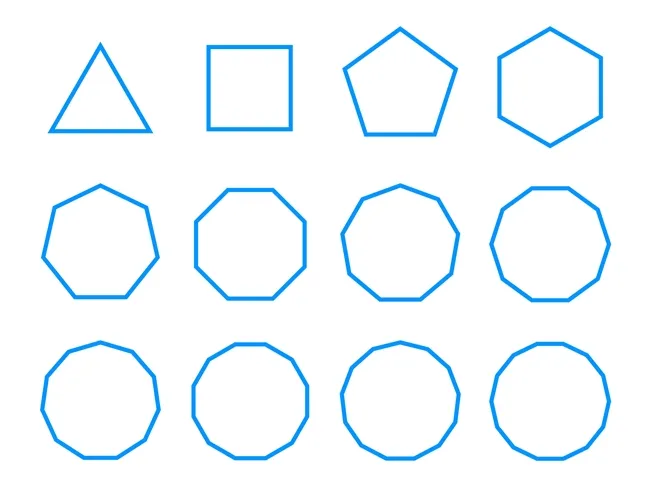
「正多角形の辺の数をどんどん増やしていくと、いつか円になるの?」という疑問を持ったことはありませんか?

今日はこの面白い疑問について、簡単に分かりやすく説明していきます!
正多角形ってどんな形?
まず、「正多角形」って何だっけ?

簡単に言うと、全部の辺が同じ長さで、全部の角が同じ大きさの多角形のことです。例えば…
- 正三角形: 全部の辺が同じ長さの三角形
- 正方形: 全部の辺が同じ長さの四角形
- 正五角形: 全部の辺が同じ長さの五角形
【少し難しいけれど面白い数学の話】
数学では正多角形のことを「正 \( n \) 角形」と呼びます。例えば正三角形は「正 3 角形」、正方形は「正 4 角形」と表します。一般的には、正 \( n \) 角形の一つの内角は次の式で求められます:
\[
\text{内角} = \frac{(n-2) \times 180}{n} \, \text{°}
\]
例えば正六角形(\( n=6 \))の内角は \( 120^\text{°} \) になります。このように、\( n \) が大きくなると一つの内角も徐々に \( 180^\text{°} \) に近づいていきますが、完全にはなりません。この性質が後で重要になります。
辺を増やすとどうなる?
次に、「正多角形の辺の数をどんどん増やしていく」とどうなるか、ちょっと想像してみましょう。
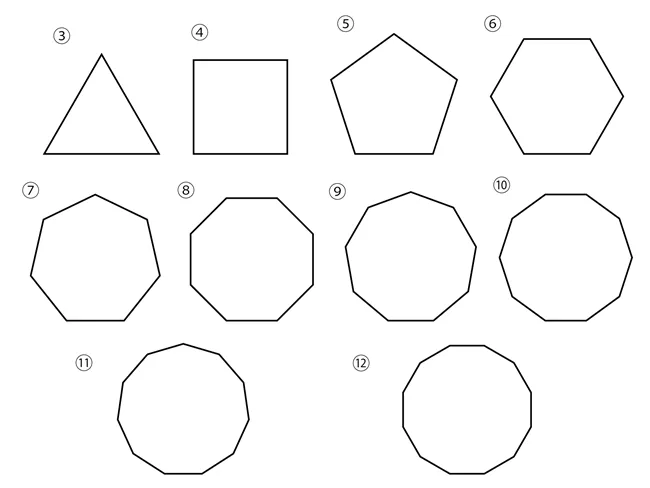
- 正三角形はカクカクした形ですね。
- 正八角形になると、少し「丸い感じ」に近づきます。
- 正十二角形を見てみると、やや円に見える。

つまり、辺の数を増やせば増やすほど、正多角形は「円に近づいていく」ことが分かります。
【少し難しいけれど面白い数学の話】
数学的には、正多角形の外接円(すべての頂点が円周上にある円)を考えると、正多角形が円に「収束」することがわかります。具体的には、以下のようなイメージです:
- 正 \( n \) 角形の周長は辺の数が増えるにつれて円周に近づいていきます。
- 辺の長さがどんどん短くなるため、頂点同士をつなぐ線が円周の一部のように見えるようになります。
数学のリミット(極限)の概念を使うと、次のように表現できます:
\[ \lim_{n \to \infty} \text{正} n \text{角形} = \text{円} \]
これは、正多角形が辺の数を無限に増やすことで、完全な円の形状に「限りなく近づく」ということを意味しています。ただし、どれだけ \( n \) を増やしても、完全に円にはならないという点が重要です。
でも、正多角形は円そのものになる?

ここで大事なポイント!

正多角形は、辺の数をどれだけ増やしても「円そのもの」にはなりません。どうしてでしょうか?
理由は簡単です!
正多角形は必ず「辺」と「角」がありますが、円にはそれがありません。どれだけ細かくても、正多角形は「辺がたくさんある形」であり、完全な曲線にはならないんです。

数学ではこれを「限りなく円に近づくだけ」と言います。
【少し難しいけれど面白い数学の話】
この現象を数式で説明すると、「具体的な \( n \) 」を指定した場合、その正 \( n \) 角形は必ず「円」ではなく、あくまで正多角形です。どの \( n \) においても次の関係が成り立ちます:
- 正 \( n \) 角形の周長 \( L_n \) は円周 \( C \) に収束します。
- ただし、正 \( n \) 角形の頂点と円周の間には必ず微小な差が存在します。
数学の世界では、「収束」しても「一致する」とは限らないことを区別します。これは、中学数学を超えた「リミット」の概念に深く関係しています。
分かりやすい例え話
正多角形が円に近づいていく様子を、身近な例で説明してみましょう。
例1:線で描く円
- 紙にコンパスを使って円を描く代わりに、短い直線をたくさんつなげて円を描こうとしてみてください。
- 最初は線が少ないのでカクカクしていますが、線の数を増やすとだんだん滑らかに見えてきます。
- しかし、どれだけ増やしても、それは「直線をつなげた形」であり、完全な曲線にはなりません。
正多角形も同じで、どんなに辺の数を増やしても、それは「多角形」であり、完全な円にはならないのです。
例2:高解像度の画面
今使っているスマホやPCの画面を思い浮かべてみてください。画面はピクセル(小さな四角形)がたくさん集まってできています。
- ピクセルが少ないと、丸いアイコンも「ギザギザ」に見えます。
- ピクセルが増える(解像度が上がる)と、丸いアイコンは滑らかに見えてきます。
でも、どれだけピクセルを細かくしても、それは「小さな四角形」が集まったもの。完全な滑らかな曲線(=円そのもの)にはならないのです。
例3:階段で坂を表現する
坂道を階段で表現することを考えてみましょう。
- 階段の段差が大きいと、「階段だな」とはっきり分かります。
- 階段の段差を小さくしていくと、「坂に見える!」となります。
でも、どれだけ段差を小さくしても、それは「段差のある階段」です。完全な坂道(=滑らかな傾斜)にはなりません。
【少し難しいけれど面白い数学の話】
これらの例え話は、数学でいう「収束」の考え方を分かりやすくしたものです。正多角形が円に近づくことは、次のような関係を表しています:
- 正 \( n \) 角形の周長や面積は、\( n \to \infty \) で円の周長や面積に収束します。
- しかし、正多角形はどの \( n \) においても「円そのもの」ではなく、あくまで「多角形」です。
このように「限りなく近づくけれど一致しない」ことをリミット(極限)と呼びます。この考え方は、高校数学や微積分の重要な基礎になります。
まとめ

今日のテーマは「正多角形が円になるのか?」という疑問でした。振り返ってみましょう!
- 正多角形とは何か
正三角形や正方形のように、すべての辺と角が等しい形のこと。辺の数を増やしていくと、形はどんどん円に近づいていきます。 - 辺を増やすとどうなるか
辺の数を増やせば増やすほど、正多角形は「円に見える」形になります。でも、正多角形には必ず「辺」と「角」があるため、どれだけ増やしても完全な円にはなりません。 - たとえ話で理解する
- 短い直線をつなげて円を描く話
- 高解像度の画面のアイコンの話
- 階段で坂を表現する話

このようなお話をして、正多角形が円に「限りなく近づくけど一致しない」という性質をイメージしてもらいました。
数学の面白さ

「正多角形がどんどん円に近づいていくけれど、完全に同じにはならない」という現象は、数学の「限りなく近づく」という考え方を表しています。
この考え方は、物事を正確に測ったり、自然現象を説明したり、未来を予測するためにとても大切です。
たとえば、円周率や自然界の動きなど、私たちの身の回りにも「無限に近づく」考え方が使われています。こうした数学の不思議が、現実世界を深く理解する手助けをしているのです。
ここから先へ

もしもっと深く知りたい場合は、「極限」「収束」「微積分」といった概念に挑戦してみてください。
高校数学や大学数学で、このような「限りなく近づくけど一致しない」現象をさらに詳しく学ぶことができます!